0. Getting started with CapyMOA

This notebook shows some basic usage of CapyMOA for supervised learning (classification and regression) * There are more detailed notebooks and documentation available, our goal here is just present some high-level functions and demonstrate a subset of CapyMOA’s functionalities. * For simplicity, we simulate data streams in the following examples using datasets and employing synthetic generators. One could also read data directly from a CSV or ARFF (See stream_from_file function)

---

More information about CapyMOA can be found in https://www.capymoa.org

last update on 25/07/2024

1. Classification

• Classification for data streams tradicionally assumes instances are available to the classifier in an incremental fashion and labels become available before a new instance becomes available

• It is common to simulate this behavior using a while loop, often referred to as a test-then-train loop which contains 4 distinct steps:

  1. Fetches the next instance from the stream

  2. Makes a prediction

  3. Train the model with the instance

  4. Update a mechanism to keep track of metrics

Some remarks about test-then-train loop: * We must not train before testing, meaning that steps 2 and 3 should not be interchanged, as this would invalidate our interpretation concerning how the model performs on unseen data, leading to unreliable evaluations of its efficacy. * Steps 3 and 4 can be completed in any order without altering the result. * What if labels are not immediately available? Then you might want to read about delayed labeling and partially labeled data, see A Survey on Semi-supervised Learning for Delayed Partially Labelled Data Streams * More information on classification for data streams is available on section 2.2 Classification from Machine Learning for Data Streams book

from capymoa.datasets import Electricity
from capymoa.evaluation import ClassificationEvaluator
from capymoa.classifier import OnlineBagging

elec_stream = Electricity()
ob_learner = OnlineBagging(schema=elec_stream.get_schema(), ensemble_size=5)
ob_evaluator = ClassificationEvaluator(schema=elec_stream.get_schema())

while elec_stream.has_more_instances():
    instance = elec_stream.next_instance()
    prediction = ob_learner.predict(instance)
    ob_learner.train(instance)
    ob_evaluator.update(instance.y_index, prediction)

print(ob_evaluator.accuracy())

82.06656073446328

1.1 High-level evaluation functions

• If our goal is just to evaluate learners it would be tedious to keep writing test-then-train loops. Thus, it makes sense to encapsulate that loop inside high-level evaluation functions.

• Furthermore, sometimes we are interested in cumulative metrics and sometimes we care about metrics windowed metrics. For example, if we want to know how accurate our model is so far, considering all the instances it has seen, then we would look at its cumulative metrics. However, we might also be interested in how well the model is every n number of instances, so that we can, for example, identify periods in which our model was really struggling to produce correct predictions.

• In this example, we use the prequential_evaluation function, which provides us with both the cumulative and the windowed metrics!

• Some remarks:

  • If you want to know more about other high-level evaluation functions, evaluators, or which metrics are available, check the 01_evaluation notebook

  • The results from evaluation functions such as prequential_evaluation follow a standard, also discussed thoroughly in the Evaluation documentation in http://www.capymoa.org

  • Sometimes authors refer to the cumulative metrics as test-then-train metrics, such as test-then-train accuracy (or TTT accuracy for short). They all refer to the same concept.

  • Shouldn’t we recreate the stream object elec_stream? No, prequential_evaluation(), by default, automatically restart() streams when they are reused.

In the below example prequential_evaluation is used with a HoeffdingTree classifier on the Electricity data stream.

from capymoa.evaluation import prequential_evaluation
from capymoa.classifier import HoeffdingTree

ht = HoeffdingTree(schema=elec_stream.get_schema(), grace_period=50)

# Obtain the results from the high-level function.
    # Note that we need to specify a window_size as we obtain both windowed and cumulative results.
    # The results from a high-level evaluation function are represented as a PrequentialResults object
results_ht = prequential_evaluation(stream=elec_stream, learner=ht, window_size=4500)

print(f"Cumulative accuracy = {results_ht.cumulative.accuracy()}, wall-clock time: {results_ht.wallclock()}")

# The windowed results are conveniently stored in a pandas DataFrame.
display(results_ht.windowed.metrics_per_window())

Cumulative accuracy = 81.6604872881356, wall-clock time: 0.25900697708129883

	instances	accuracy	kappa	kappa_t	kappa_m	f1_score	f1_score_0	f1_score_1	precision	precision_0	precision_1	recall	recall_0	recall_1
0	4500.0	87.777778	74.440796	24.242424	68.856172	87.222016	84.550562	89.889706	87.149807	84.078212	90.221402	87.294344	85.028249	89.560440
1	9000.0	83.666667	66.963969	2.649007	64.458414	83.538542	81.657100	85.279391	83.752489	84.373388	83.131589	83.325685	79.110251	87.541118
2	13500.0	85.644444	71.282626	2.269289	70.009285	85.663875	85.304823	85.968723	85.634554	83.780161	87.488948	85.693216	86.886006	84.500427
3	18000.0	81.977778	61.953129	-25.154321	57.021728	81.463331	76.168087	85.510095	82.841248	85.488127	80.194370	80.130502	68.680445	91.580559
4	22500.0	86.177778	70.202882	13.370474	64.719229	85.389296	80.931944	89.159986	86.648480	88.058706	85.238254	84.166185	74.872377	93.459993
5	27000.0	78.088889	53.951820	-72.377622	47.272727	77.186522	71.634062	82.150615	77.962693	77.521793	78.403594	76.425652	66.577540	86.273764
6	31500.0	79.066667	55.619360	-71.897810	46.263548	77.829775	72.504378	83.100108	78.081099	74.237896	81.924301	77.580064	70.849971	84.310157
7	36000.0	74.955556	49.002474	-89.411765	37.354086	74.661963	70.719667	78.120753	74.256346	66.390244	82.122449	75.072035	75.653141	74.490929
8	40500.0	74.555556	50.130218	-71.664168	41.312148	76.116886	74.818562	74.286998	76.196815	65.523883	86.869748	76.037125	87.186058	64.888191
9	45000.0	84.377778	68.535062	-0.428571	68.390288	84.268304	82.949309	85.585401	84.249034	82.648623	85.849445	84.287584	83.252191	85.322976
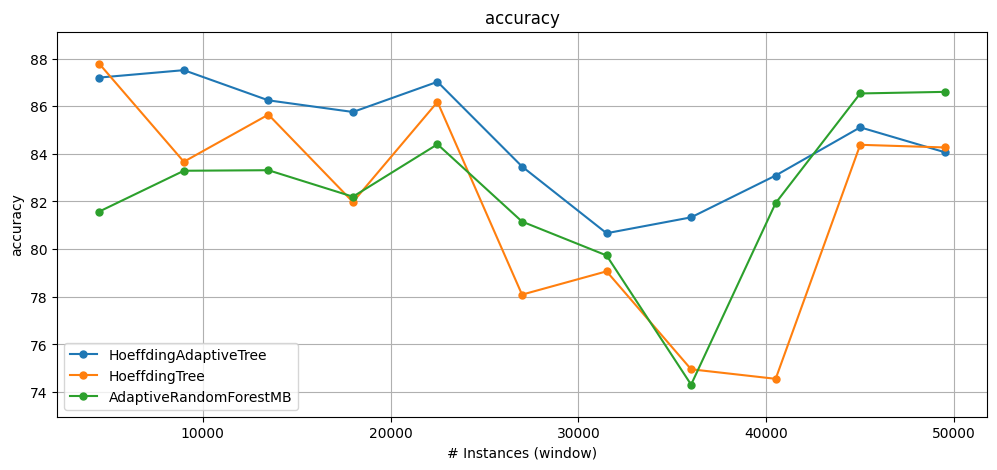
10	45312.0	84.266667	68.237903	-2.757620	67.876588	84.118966	82.587309	85.650588	84.121918	82.627953	85.615883	84.116013	82.546706	85.685320

1.2 Comparing results among classifiers

• CapyMOA provides plot_windowed_results as an easy visualization function for quickly comparing windowed metrics

• In the example below, we create three classifiers: HoeffdingAdaptiveTree, HoeffdingTree and AdaptiveRandomForest, and plot the results using plot_windowed_results

• More details about plot_windowed_results options are described in the documentation: http://www.capymoa.org

from capymoa.evaluation.visualization import plot_windowed_results
from capymoa.base import MOAClassifier
from moa.classifiers.trees import HoeffdingAdaptiveTree
from capymoa.classifier import HoeffdingTree
from capymoa.classifier import AdaptiveRandomForestClassifier

# Create the wrapper for HoeffdingAdaptiveTree (from MOA)
HAT = MOAClassifier(schema=elec_stream.get_schema(), moa_learner=HoeffdingAdaptiveTree, CLI="-g 50")
HT = HoeffdingTree(schema=elec_stream.get_schema(), grace_period=50)
ARF = AdaptiveRandomForestClassifier(schema=elec_stream.get_schema(), ensemble_size=10, number_of_jobs=4)

results_HAT = prequential_evaluation(stream=elec_stream, learner=HAT, window_size=4500)
results_HT = prequential_evaluation(stream=elec_stream, learner=HT, window_size=4500)
results_ARF = prequential_evaluation(stream=elec_stream, learner=ARF, window_size=4500)

# Comparing models based on their cumulative accuracy
print(f"HAT accuracy = {results_HAT.cumulative.accuracy()}")
print(f"HT accuracy = {results_HT.cumulative.accuracy()}")
print(f"ARF accuracy = {results_ARF.cumulative.accuracy()}")

# Plotting the results. Note that we ovewrote the ylabel, but that doesn't change the metric.
plot_windowed_results(results_HAT, results_HT, results_ARF, metric="accuracy", xlabel="# Instances (window)")

HAT accuracy = 84.68617584745762
HT accuracy = 81.6604872881356
ARF accuracy = 81.90766242937853

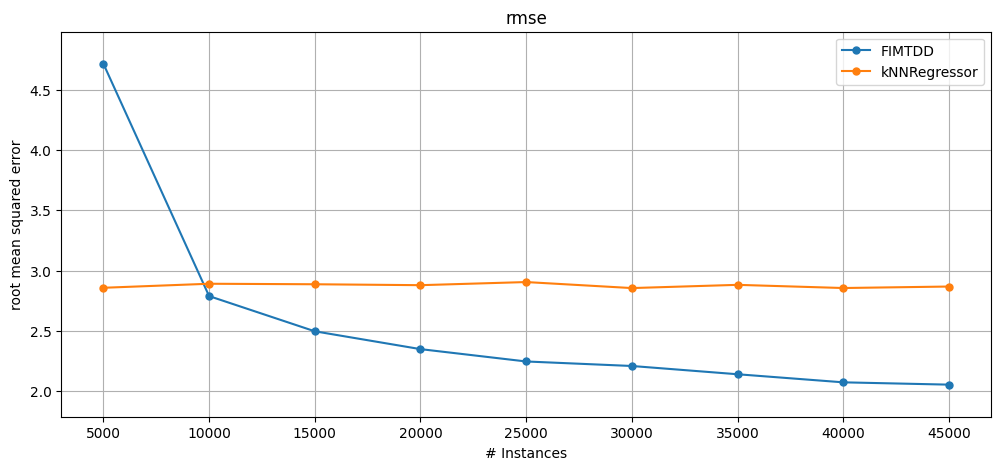
2. Regression

• Regression algorithms have its API usage very similar to classification algorithms. We can use the same high-level evaluation and visualization functions for regression and classification.

• Similarly to classification, we can also use MOA objects through a generic API.

from capymoa.datasets import Fried
from moa.classifiers.trees import FIMTDD
from capymoa.base import MOARegressor
from capymoa.regressor import KNNRegressor

fried_stream = Fried()  # Downloads the Fried dataset into the data dir in case it is not there yet.
fimtdd = MOARegressor(schema=fried_stream.get_schema(), moa_learner=FIMTDD())
knnreg = KNNRegressor(schema=fried_stream.get_schema(), k=3, window_size=1000)

results_fimtdd = prequential_evaluation(stream=fried_stream, learner=fimtdd, window_size=5000)
results_knnreg = prequential_evaluation(stream=fried_stream, learner=knnreg, window_size=5000)

results_fimtdd.windowed.metrics_per_window()
# Note that the metric is different from the ylabel parameter, which just overrides the y-axis label.
plot_windowed_results(results_fimtdd, results_knnreg, metric="rmse", ylabel="root mean squared error")

3. Concept Drift

• One of the most challenging and defining aspects of data streams is the phenomenon known as concept drifts.

• In CapyMOA, we designed the simplest and most complete API for simulating, visualizing and assessing concept drifts.

• In the example below we focus on a simple way of simulating and visualizing a drifting stream. There is a tutorial focusing entirely on how Concept Drift can be simulated, detected and assessed in a separate notebook (See Tutorial 4: Simulating Concept Drifts with the DriftStream API)

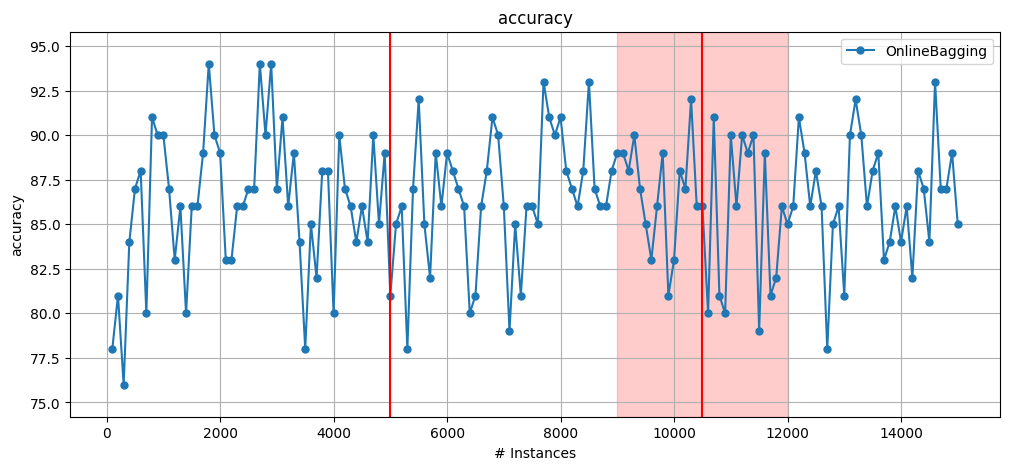
3.1 Plotting Drift Detection results

• This example uses the DriftStream building API, precisely the positional version where drifts are specified according to their exact location on the stream.

• Integration with the visualization function. The DriftStream object carries meta-information about the drift which is passed along the stream and thus become available to plot_windowed_results

• The following plot contains two drifts: 1 abrupt and 1 gradual, such that the abrupt drift is located at instance 5000 and the gradual drift starts at instance 9000 and ends at 12000. This information is provided to the stream via GradualDrift(start=9000, end=12000)

• More details concerning Concept Drift in CapyMOA can be found in the documentation: http://www.capymoa.org

from capymoa.classifier import OnlineBagging
from capymoa.stream.generator import SEA
from capymoa.stream.drift import Drift, AbruptDrift, GradualDrift, DriftStream

# Generating a synthetic stream with 1 abrupt drift and 1 gradual drift.
stream_sea2drift = DriftStream(stream=[SEA(function=1),
                                AbruptDrift(position=5000),
                                SEA(function=3),
                                GradualDrift(start=9000, end=12000),
                                SEA(function=1)])

OB = OnlineBagging(schema=stream_sea2drift.get_schema(), ensemble_size=10)

# Since this is a synthetic stream, max_instances is needed to determine the amount of instances to be generated.
results_sea2drift_OB = prequential_evaluation(stream=stream_sea2drift, learner=OB, window_size=100, max_instances=15000)

# print(stream_sea2drift.drifts)
plot_windowed_results(results_sea2drift_OB, metric="accuracy")

None