Anomaly Detection

This notebook shows some basic usage of CapyMOA for anomaly detection tasks.

Algorithms: HalfSpaceTrees, Autoencoder and Online Isolation Forest

Important notes: Prior to version 0.8.2, a lower anomaly score indicated a higher likelihood of an anomaly. This has been updated so that a higher anomaly score now indicates a higher likelihood of an anomaly, aligning with the standard anomaly detection literature.

---

More information about CapyMOA can be found at https://www.capymoa.org.

last update on 28/11/2025

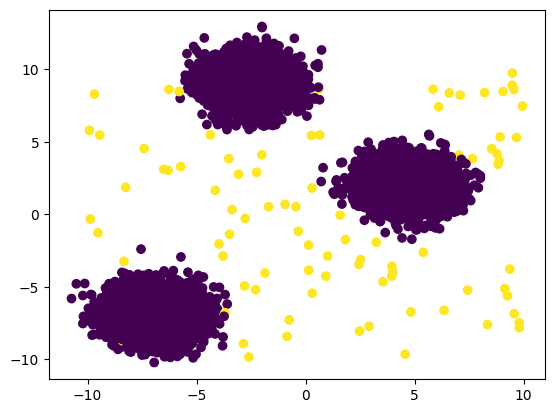
1. Creating simple anomalous data with sklearn

• Generating a few examples and some simple anomalous data using sklearn.

import numpy as np
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from capymoa.stream import NumpyStream

# generate normal data points
n_samples = 10000
n_features = 2
n_clusters = 3
X, y = make_blobs(
    n_samples=n_samples, n_features=n_features, centers=n_clusters, random_state=42
)

# generate anomalous data points
n_anomalies = 100  # the anomaly rate is 1%
anomalies = np.random.uniform(low=-10, high=10, size=(n_anomalies, n_features))

# combine the normal data points with anomalies
X = np.vstack([X, anomalies])
y = np.hstack([y, [1] * n_anomalies])  # Label anomalies with 1
y[:n_samples] = 0  # Label normal points with 0

# shuffle the data
idx = np.random.permutation(n_samples + n_anomalies)
X = X[idx]
y = y[idx]

plt.scatter(X[:, 0], X[:, 1], c=y, cmap="viridis")
plt.show()

# create a NumpyStream from the combined dataset
feature_names = [f"feature_{i}" for i in range(n_features)]
target_name = "class"

2. Unsupervised anomaly detection for data streams

• Recent research has been focused on unsupervised anomaly detection for data streams, as it is often difficult to obtain labeled data for training.

• Instead of using evaluation functions, we first use a basic test-then-train loop from scratch to evaluate the model’s performance.

• Please note that higher scores indicate higher anomaly likelihood.

from capymoa.anomaly import HalfSpaceTrees
from capymoa.evaluation import AnomalyDetectionEvaluator

stream_ad = NumpyStream(
    X,
    y,
    dataset_name="AnomalyDetectionDataset",
    feature_names=feature_names,
    target_name=target_name,
    target_type="categorical",
)
learner = HalfSpaceTrees(stream_ad.get_schema())
evaluator = AnomalyDetectionEvaluator(stream_ad.get_schema())
while stream_ad.has_more_instances():
    instance = stream_ad.next_instance()
    score = learner.score_instance(instance)
    evaluator.update(instance.y_index, score)
    learner.train(instance)

auc = evaluator.auc()
print(f"AUC: {auc:.2f}")

AUC: 0.95

3. High-level evaluation functions

• CapyMOA provides prequential_evaluation_anomaly as a high level function to assess anomaly detectors.

3.1 prequential_evaluation_anomaly

In this example, we use the prequential_evaluation_anomaly function with plot_windowed_results to plot AUC for HalfSpaceTrees on the synthetic data stream.

from capymoa.evaluation.visualization import plot_windowed_results
from capymoa.anomaly import HalfSpaceTrees
from capymoa.evaluation import prequential_evaluation_anomaly

stream_ad = NumpyStream(
    X,
    y,
    dataset_name="AnomalyDetectionDataset",
    feature_names=feature_names,
    target_name=target_name,
    target_type="categorical",
)
hst = HalfSpaceTrees(schema=stream_ad.get_schema())

results_hst = prequential_evaluation_anomaly(
    stream=stream_ad, learner=hst, window_size=1000
)

print(f"AUC: {results_hst.auc()}")
display(results_hst.windowed.metrics_per_window())
plot_windowed_results(results_hst, metric="auc", save_only=False)

AUC: 0.948493

	instances	auc	s_auc	Accuracy	Kappa	Periodical holdout AUC	Pos/Neg ratio	G-Mean	Recall	KappaM
0	1000.0	0.874663	0.182711	0.064	0.001332	0.000000	0.012146	0.229416	1.0	-77.000000
1	2000.0	0.961608	0.210984	0.005	0.000000	0.874663	0.005025	0.000000	1.0	-116.058824
2	3000.0	0.968539	0.218827	0.012	0.000000	0.961608	0.012146	0.000000	1.0	-101.206897
3	4000.0	0.951515	0.217991	0.010	0.000000	0.968539	0.010101	0.000000	1.0	-100.538462
4	5000.0	0.964196	0.188622	0.015	0.000000	0.951515	0.015228	0.000000	1.0	-90.203704
5	6000.0	0.992161	0.212583	0.005	0.000000	0.964196	0.005025	0.000000	1.0	-100.186441
6	7000.0	0.958268	0.205480	0.011	0.000000	0.992161	0.011122	0.000000	1.0	-97.900000
7	8000.0	0.953488	0.210055	0.011	0.000000	0.958268	0.011122	0.000000	1.0	-96.679012
8	9000.0	0.933216	0.168399	0.008	0.000000	0.953488	0.008065	0.000000	1.0	-99.314607
9	10000.0	0.981708	0.214861	0.011	0.000000	0.933216	0.011122	0.000000	1.0	-97.900000
10	10100.0	0.980973	0.213611	0.011	0.000000	0.981708	0.011122	0.000000	1.0	-98.889000

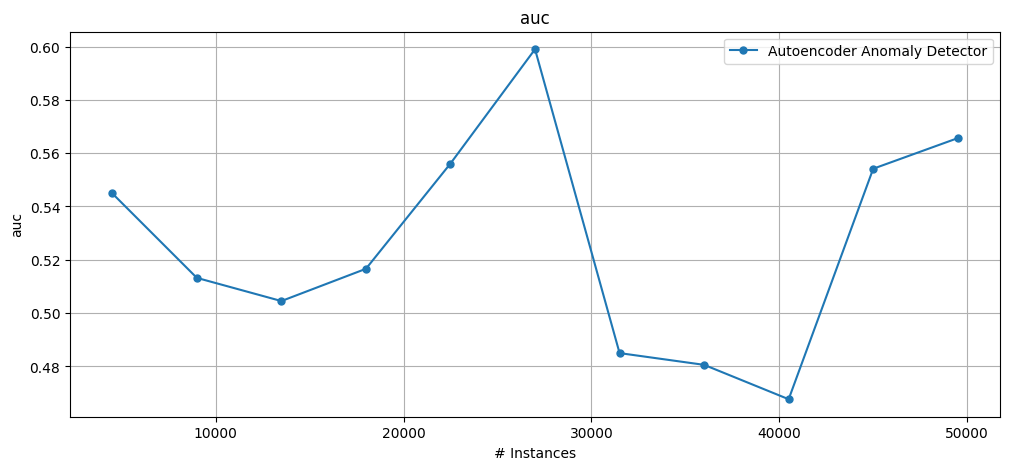
3.2 Autoencoder

from capymoa.evaluation.visualization import plot_windowed_results
from capymoa.anomaly import Autoencoder
from capymoa.evaluation import prequential_evaluation_anomaly

stream_ad = NumpyStream(
    X,
    y,
    dataset_name="AnomalyDetectionDataset",
    feature_names=feature_names,
    target_name=target_name,
    target_type="categorical",
)
ae = Autoencoder(schema=stream_ad.get_schema(), hidden_layer=1)

results_ae = prequential_evaluation_anomaly(
    stream=stream_ad, learner=ae, window_size=1000
)

print(f"AUC: {results_ae.auc()}")
display(results_ae.windowed.metrics_per_window())
plot_windowed_results(results_ae, metric="auc", save_only=False)

AUC: 0.562556

	instances	auc	s_auc	Accuracy	Kappa	Periodical holdout AUC	Pos/Neg ratio	G-Mean	Recall	KappaM
0	1000.0	0.608384	1.089317e-04	0.987	-0.001850	0.000000	0.012146	0.000000	0.0	-0.083333
1	2000.0	0.649447	5.898215e-06	0.994	-0.001669	0.608384	0.005025	0.000000	0.0	0.294118
2	3000.0	0.588310	5.939977e-03	0.987	-0.001850	0.649447	0.012146	0.000000	0.0	-0.344828
3	4000.0	0.534747	5.589712e-02	0.991	0.180328	0.588310	0.010101	0.316228	0.1	0.076923
4	5000.0	0.458883	8.677773e-04	0.985	0.000000	0.534747	0.015228	0.000000	0.0	-0.388889
5	6000.0	0.465729	9.141556e-07	0.994	-0.001669	0.458883	0.005025	0.000000	0.0	0.389831
6	7000.0	0.627815	4.753149e-02	0.989	0.000000	0.465729	0.011122	0.000000	0.0	-0.100000
7	8000.0	0.651163	2.229827e-05	0.988	-0.001837	0.627815	0.011122	0.000000	0.0	-0.185185
8	9000.0	0.504662	3.494982e-03	0.992	0.000000	0.651163	0.008065	0.000000	0.0	0.191011
9	10000.0	0.546190	6.503471e-07	0.989	0.000000	0.504662	0.011122	0.000000	0.0	-0.100000
10	10100.0	0.542053	6.478350e-07	0.989	0.000000	0.546190	0.011122	0.000000	0.0	-0.111000

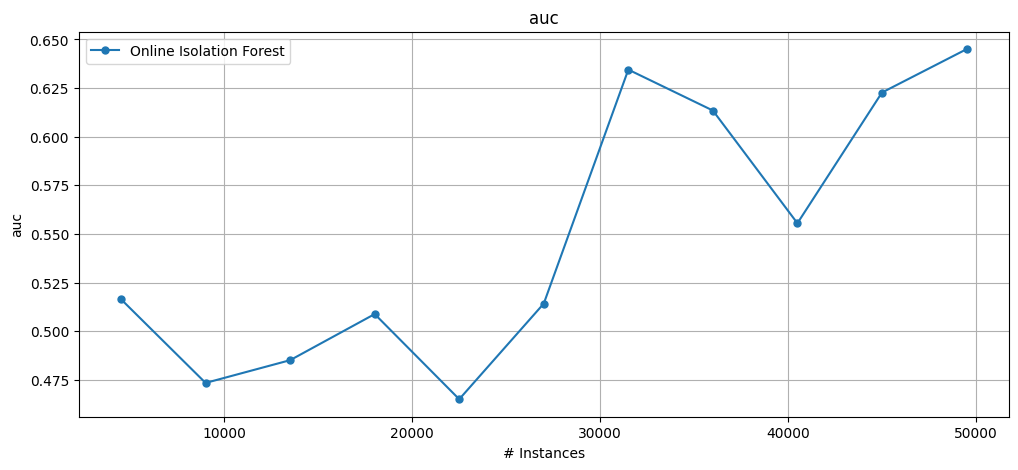
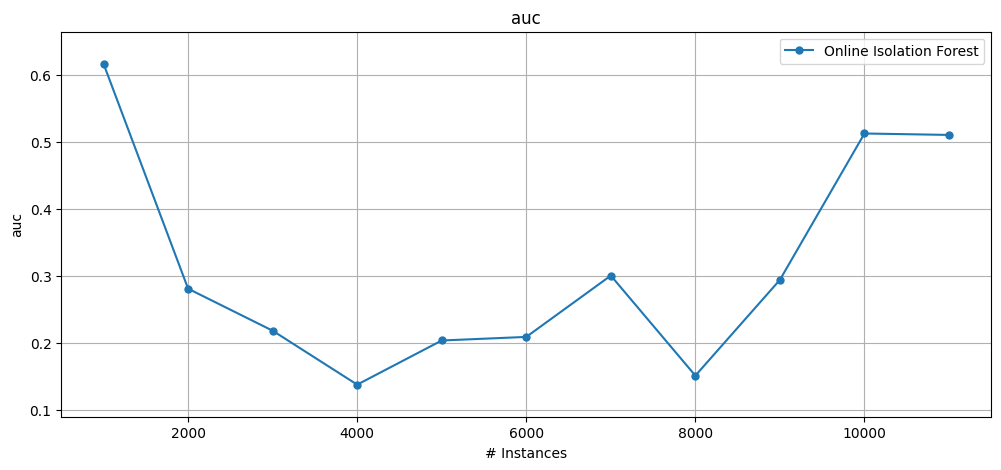
3.3 Online Isolation Forest

from capymoa.evaluation.visualization import plot_windowed_results
from capymoa.anomaly import OnlineIsolationForest
from capymoa.evaluation import prequential_evaluation_anomaly

stream_ad = NumpyStream(
    X,
    y,
    dataset_name="AnomalyDetectionDataset",
    feature_names=feature_names,
    target_name=target_name,
    target_type="categorical",
)
oif = OnlineIsolationForest(schema=stream_ad.get_schema(), num_trees=10)

results_oif = prequential_evaluation_anomaly(
    stream=stream_ad, learner=oif, window_size=1000
)

print(f"AUC: {results_oif.auc()}")
display(results_oif.windowed.metrics_per_window())
plot_windowed_results(results_oif, metric="auc", save_only=False)

AUC: 0.827975

	instances	auc	s_auc	Accuracy	Kappa	Periodical holdout AUC	Pos/Neg ratio	G-Mean	Recall	KappaM
0	1000.0	0.699393	0.037054	0.955	-0.017915	0.000000	0.012146	0.0	0.0	-2.750000
1	2000.0	0.840603	0.061799	0.995	0.000000	0.699393	0.005025	0.0	0.0	0.411765
2	3000.0	0.829791	0.065623	0.988	0.000000	0.840603	0.012146	0.0	0.0	-0.241379
3	4000.0	0.832727	0.052678	0.990	0.000000	0.829791	0.010101	0.0	0.0	-0.025641
4	5000.0	0.921083	0.076654	0.985	0.000000	0.832727	0.015228	0.0	0.0	-0.388889
5	6000.0	0.996985	0.114542	0.995	0.000000	0.921083	0.005025	0.0	0.0	0.491525
6	7000.0	0.871955	0.045403	0.989	0.000000	0.996985	0.011122	0.0	0.0	-0.100000
7	8000.0	0.854582	0.053205	0.989	0.000000	0.871955	0.011122	0.0	0.0	-0.086420
8	9000.0	0.515121	0.018523	0.992	0.000000	0.854582	0.008065	0.0	0.0	0.191011
9	10000.0	0.983638	0.093084	0.989	0.000000	0.515121	0.011122	0.0	0.0	-0.100000
10	10100.0	0.984925	0.093285	0.989	0.000000	0.983638	0.011122	0.0	0.0	-0.111000

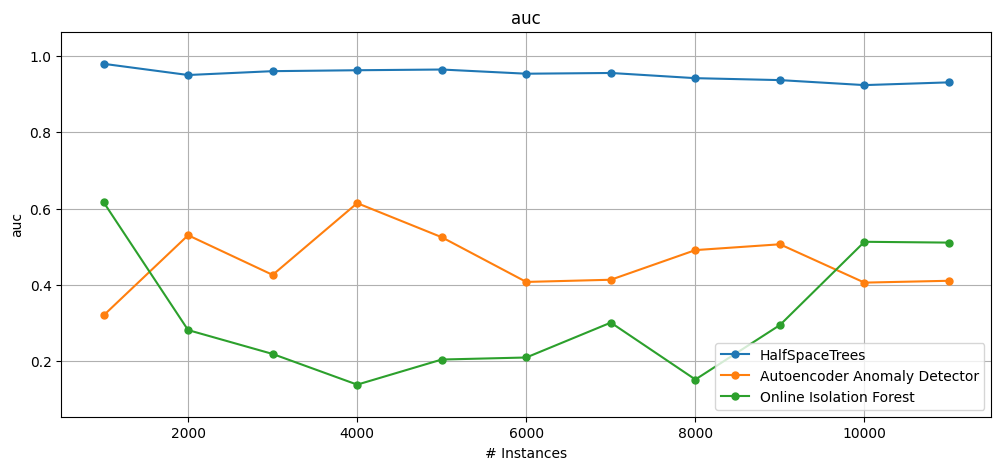
4. Comparing algorithms

plot_windowed_results(
    results_hst, results_ae, results_oif, metric="auc", save_only=False
)