Parallel ensembles

This notebook is aimed at showing how to use the parallel and mini-batch variants of the ensembles and includes:

• Examples of all the available parallel ensembles.

• Examples on how to use the parallel versions.

• Examples of the trade-offs between runtime and accuracy when using the parallel ensembles.

Please note that this notebook may take a while to execute as it processes hundreds of thousands of instances with ensembles of up to 100 learners.

---

More information about CapyMOA can be found at https://www.capymoa.org.

last update on 01/12/2025

1. Using the most basic bagging ensemble

• CapyMOA chooses between the standard and the mini-batch version behind the curtains based on the parameter configuration used.

• For more information about the parallel ensembles please refer to the following references:

  7. Cassales, H. M. Gomes, A. Bifet, B. Pfahringer and H. Senger, Improving the performance of bagging ensembles for data streams through mini-batching, Information Sciences,Volume 580, 2021, Pages 260-282, ISSN 0020-0255, https://doi.org/10.1016/j.ins.2021.08.085.

  7. Cassales, H. M. Gomes, A. Bifet, B. Pfahringer and H. Senger, “Balancing Performance and Energy Consumption of Bagging Ensembles for the Classification of Data Streams in Edge Computing,” in IEEE Transactions on Network and Service Management, vol. 20, no. 3, pp. 3038-3054, Sept. 2023, doi: 10.1109/TNSM.2022.3226505.

1.1 Understanding the parameters

• Since we used different parameters in the constructor call, each instance references a different object:

  • sequential: note the CLI help only mentions baseLearner and ensembleSize.

  • parallel: note the extra parameters numCores and batchSize.

• Setting the parallel parameters on the constructor call will make it a mini-batch parallel ensemble.

print(ozabag_sequential.cli_help())

-l baseLearner (default: trees.HoeffdingTree)
Classifier to train.
-s ensembleSize (default: 10)
The number of models in the bag.

print(ozabag_mb_parallel.cli_help())

-l baseLearner (default: trees.HoeffdingTree)
Classifier to train.
-s ensembleSize (default: 10)
The number of models in the bag.
-c numCores (default: 1)
The amount of CPU Cores used for multi-threading
-b batchSize (default: 1)
The amount of instances the classifier should buffer before training.

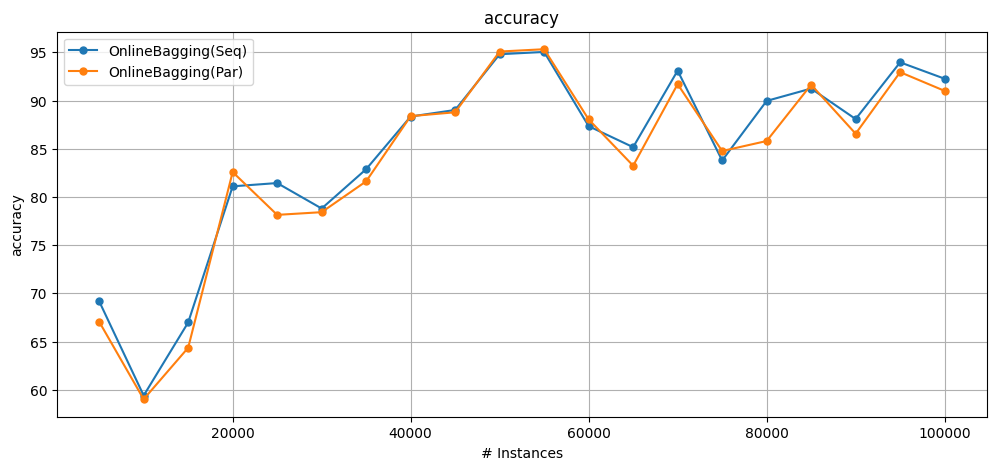
1.2 Example comparing sequential and parallel

result_seq = prequential_evaluation(
    stream=cover,
    learner=ozabag_sequential,
    window_size=window_size,
    max_instances=max_instances,
)
result_par = prequential_evaluation(
    stream=cover,
    learner=ozabag_mb_parallel,
    window_size=window_size,
    max_instances=max_instances,
)

result_seq.learner = "OnlineBagging(Seq)"
result_par.learner = "OnlineBagging(Par)"

• Note that the mini-batch approach creates a divergence in the results for two reasons:

  1. It uses local random generators instead of a global one.

  2. The mini-batch defers the model update by a few instances which causes differences in the predictions.

• On the bright side, it also decreases runtime.

# decoupling the running and plotting to allow more flexibility
print(f"Cumulative accuracy = {result_seq['cumulative'].accuracy()}")
print(f"wallclock = {result_seq['wallclock']} seconds\n")
print(f"Cumulative accuracy = {result_par['cumulative'].accuracy()}")
print(f"wallclock = {result_par['wallclock']} seconds\n")
plot_windowed_results(result_seq, result_par, metric="accuracy")

Cumulative accuracy = 84.59299999999999
wallclock = 8.546567440032959 seconds

Cumulative accuracy = 83.722
wallclock = 6.080326557159424 seconds

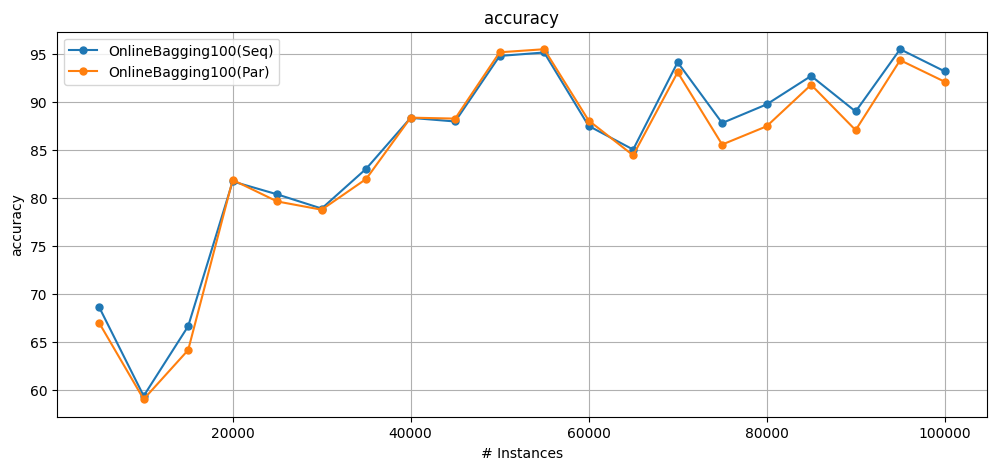
1.3 Increasing the ensemble size

• Ensembles with more learners will get a bigger decrease in processing time.

• Let’s see the difference when using 100 classifiers.

ozabag_sequential = OnlineBagging(schema=cover.schema, ensemble_size=100)
ozabag_mb_parallel = OnlineBagging(
    schema=cover.schema, ensemble_size=100, minibatch_size=25, number_of_jobs=5
)
result_seq100 = prequential_evaluation(
    stream=cover,
    learner=ozabag_sequential,
    window_size=window_size,
    max_instances=max_instances,
)
result_par100 = prequential_evaluation(
    stream=cover,
    learner=ozabag_mb_parallel,
    window_size=window_size,
    max_instances=max_instances,
)

result_seq100.learner = "OnlineBagging100(Seq)"
result_par100.learner = "OnlineBagging100(Par)"

# decoupling the running and plotting to allow more flexibility
print(f"Cumulative accuracy = {result_seq100['cumulative'].accuracy()}")
print(f"wallclock = {result_seq100['wallclock']} seconds\n")
print(f"Cumulative accuracy = {result_par100['cumulative'].accuracy()}")
print(f"wallclock = {result_par100['wallclock']} seconds\n")
plot_windowed_results(result_seq100, result_par100, metric="accuracy")

Cumulative accuracy = 84.99600000000001
wallclock = 75.55597376823425 seconds

Cumulative accuracy = 84.20299999999999
wallclock = 45.28148531913757 seconds

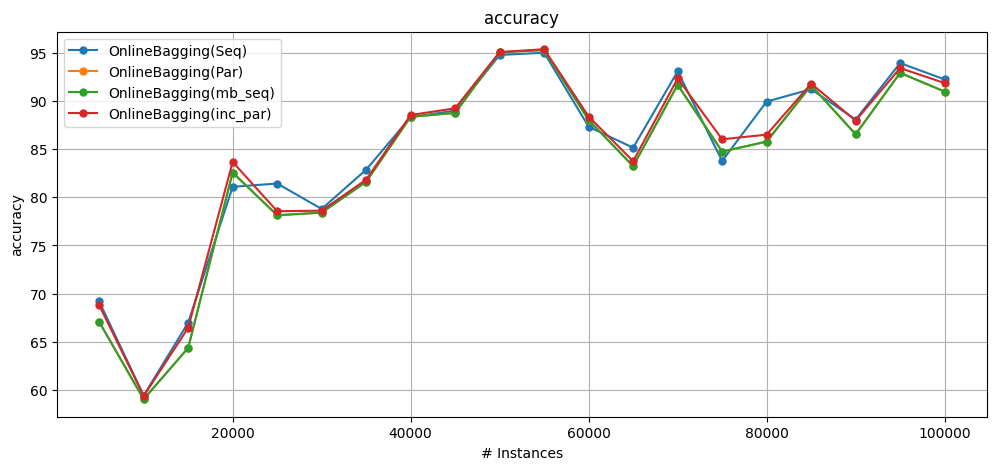
2. Other variations

In this section we show:

• Sequential execution with mini-batches.

• Parallel execution of the incremental approach.

mbSeq = OnlineBagging(schema=cover.get_schema(), ensemble_size=10, minibatch_size=25)
incPar = OnlineBagging(
    schema=cover.get_schema(), ensemble_size=10, minibatch_size=1, number_of_jobs=5
)
result_mbSeq = prequential_evaluation(
    stream=cover, learner=mbSeq, window_size=window_size, max_instances=max_instances
)
result_incPar = prequential_evaluation(
    stream=cover, learner=incPar, window_size=window_size, max_instances=max_instances
)

result_mbSeq.learner = "OnlineBagging(mb_seq)"
result_incPar.learner = "OnlineBagging(inc_par)"

• Incremental Sequential differs from Incremental Parallel because of the random sequences.

• When compared among themselves, mini-batch parallel and mini-batch sequential (single-core) have the same accuracy, as their random sequences are initialised in the same way.

• Incremental Parallel has the same random sequences as the mini-batch version - its improvement comes from making all of the predictions with the most up-to-date model.

# decoupling the running and plotting to allow more flexibility
print("Incremental Sequential ")
print(f"Cumulative accuracy = {result_seq['cumulative'].accuracy()}")
print(f"wallclock = {result_seq['wallclock']} seconds\n")
print("Mini-batch Parallel")
print(f"Cumulative accuracy = {result_par['cumulative'].accuracy()}")
print(f"wallclock = {result_par['wallclock']} seconds\n")
print("Mini-batch Sequential")
print(f"Cumulative accuracy = {result_mbSeq['cumulative'].accuracy()}")
print(f"wallclock = {result_mbSeq['wallclock']} seconds\n")
print("Incremental Parallel ")
print(f"Cumulative accuracy = {result_incPar['cumulative'].accuracy()}")
print(f"wallclock = {result_incPar['wallclock']} seconds\n")
plot_windowed_results(
    result_seq, result_par, result_mbSeq, result_incPar, metric="accuracy"
)

Incremental Sequential
Cumulative accuracy = 84.59299999999999
wallclock = 8.546567440032959 seconds

Mini-batch Parallel
Cumulative accuracy = 83.722
wallclock = 6.080326557159424 seconds

Mini-batch Sequential
Cumulative accuracy = 83.722
wallclock = 8.373425006866455 seconds

Incremental Parallel
Cumulative accuracy = 84.391
wallclock = 9.659797430038452 seconds

3. More ensembles

There are more mini-batch ensembles with parallelism implemented such as:

• AdaptiveRandomForest

• LeveragingBagging

• OzaBagAdwin

from capymoa.classifier import (
    OnlineAdwinBagging,
    LeveragingBagging,
    AdaptiveRandomForestClassifier,
)

ob_adwin = OnlineAdwinBagging(schema=cover.get_schema(), ensemble_size=30)
lb = LeveragingBagging(schema=cover.get_schema(), ensemble_size=30)
arf = AdaptiveRandomForestClassifier(schema=cover.get_schema(), ensemble_size=30)

results_ob_adwin = prequential_evaluation(
    stream=cover, learner=ob_adwin, window_size=window_size, max_instances=max_instances
)
results_lb = prequential_evaluation(
    stream=cover, learner=lb, window_size=window_size, max_instances=max_instances
)
results_arf = prequential_evaluation(
    stream=cover, learner=arf, window_size=window_size, max_instances=max_instances
)

print(
    f"Accuracy {results_ob_adwin['learner']}: {results_ob_adwin['cumulative'].accuracy()}"
)
print(f"Accuracy {results_lb['learner']}: {results_lb['cumulative'].accuracy()}")
print(f"Accuracy {results_arf['learner']}: {results_arf['cumulative'].accuracy()}")

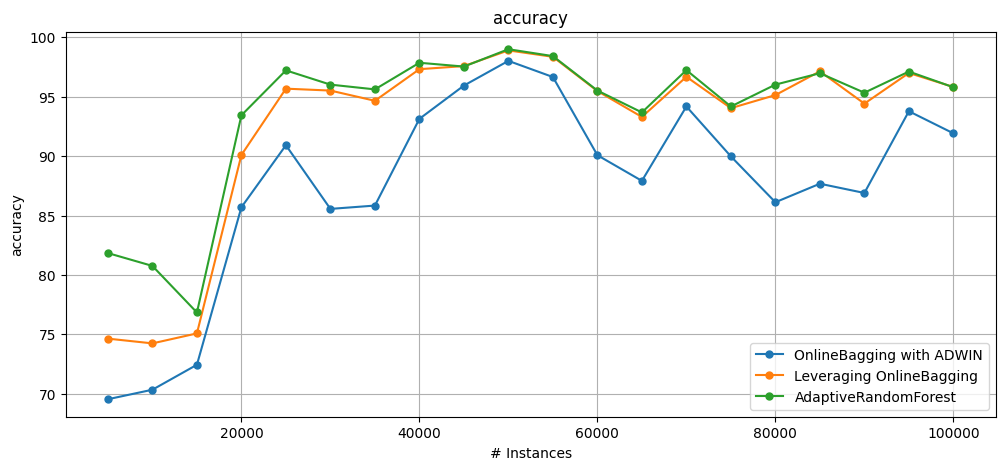
plot_windowed_results(results_ob_adwin, results_lb, results_arf, metric="accuracy")

Accuracy OnlineBagging with ADWIN: 87.63300000000001
Accuracy Leveraging OnlineBagging: 92.55499999999999
Accuracy AdaptiveRandomForest: 93.826

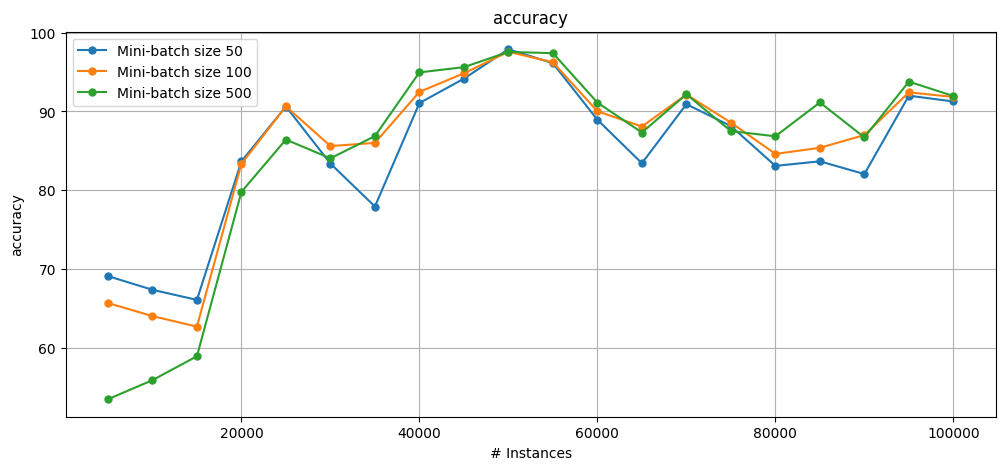
4. Mini-batch size impact

• The greater the mini-batch size, the greater the impact on performance (both good and bad).

• Although this behavior can fluctuate during the stream, at the end it is expected that larger mini-batches have a slightly smaller runtime and slightly worse accuracy.

  • It becomes slightly faster due to the reuse of data structures in the higher memory hierarchy.

  • Predictions are slightly worse due to the larger number of instances predicted with the “outdated” model.

    • Especially in the case of concept drifts, which suffer from the delay in detection and reset of the classifier.

ob_adwin_mb50 = OnlineAdwinBagging(
    schema=cover.get_schema(), ensemble_size=30, minibatch_size=50, number_of_jobs=5
)
ob_adwin_mb100 = OnlineAdwinBagging(
    schema=cover.get_schema(), ensemble_size=30, minibatch_size=100, number_of_jobs=5
)
ob_adwin_mb500 = OnlineAdwinBagging(
    schema=cover.get_schema(), ensemble_size=30, minibatch_size=500, number_of_jobs=5
)

results_ob_adwin_mb50 = prequential_evaluation(
    stream=cover,
    learner=ob_adwin_mb50,
    window_size=window_size,
    max_instances=max_instances,
)
results_ob_adwin_mb100 = prequential_evaluation(
    stream=cover,
    learner=ob_adwin_mb100,
    window_size=window_size,
    max_instances=max_instances,
)
results_ob_adwin_mb500 = prequential_evaluation(
    stream=cover,
    learner=ob_adwin_mb500,
    window_size=window_size,
    max_instances=max_instances,
)

results_ob_adwin_mb50.learner = "Mini-batch size 50"
results_ob_adwin_mb100.learner = "Mini-batch size 100"
results_ob_adwin_mb500.learner = "Mini-batch size 500"

print(
    f"Accuracy {results_ob_adwin_mb50['experiment_id']}: {results_ob_adwin_mb50['cumulative'].accuracy()}"
)
print(f"wallclock = {results_ob_adwin_mb50['wallclock']} seconds\n")
print(
    f"Accuracy {results_ob_adwin_mb100['experiment_id']}: {results_ob_adwin_mb100['cumulative'].accuracy()}"
)
print(f"wallclock = {results_ob_adwin_mb100['wallclock']} seconds\n")
print(
    f"Accuracy {results_ob_adwin_mb500['experiment_id']}: {results_ob_adwin_mb500['cumulative'].accuracy()}"
)
print(f"wallclock = {results_ob_adwin_mb500['wallclock']} seconds\n")

plot_windowed_results(
    results_ob_adwin_mb50,
    results_ob_adwin_mb100,
    results_ob_adwin_mb500,
    metric="accuracy",
)

Accuracy None: 85.038
wallclock = 15.45273756980896 seconds

Accuracy None: 85.954
wallclock = 13.486253023147583 seconds

Accuracy None: 84.97200000000001
wallclock = 12.69246792793274 seconds